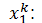LP_SOLVE

Lp_solve es un programa que resuelve problemas de programación lineal entera mixta (MLP).

Fue desarrollado originalmente por Michel Berkelaar en Eindhoven University of Technology. Jeroen Dirks hizo que la transición de la versión básica 1.5 a la versión completa 2.0 fuera posible. Él contribuyó la interfaz de procedimiento, un built-in lector MPS, y muchas correcciones y mejoras en el código.

lp_solve es una biblioteca que consta de un conjunto de rutinas, llamadas API que se puede llamar desde casi cualquier lenguaje de programación para resolver problemas MILP.

Hay varias formas de pasar los datos a la biblioteca:

·         A través de la API.

·         A través de los archivos de entrada.

·         A través de un IDE.

El API es un conjunto de rutinas que se pueden llamar desde un lenguaje de programación para construir el modelo en la memoria, resolver y devolver los resultados. Hay muchas rutinas de la API para realizar muchas tareas posibles y establecer varias opciones.

A través de los archivos de entrada, soporta varios tipos de archivos de entrada. El formato común conocido como MPS es un apoyo de la mayoría de resolver, pero no es muy legible para los seres humanos.

Otro formato es el formato lp que es más legible. lp_solve tiene la capacidad única de utilizar rutinas escritas por el usuario para introducir el modelo.

A través de un IDE gracias a Henri Gourvest, ahora hay también un programa llamado IDE LPSolve; IDE que utiliza la API para proporcionar una aplicación de Windows para resolver los modelos. Con este programa usted no tiene que saber nada de la API o de lenguajes de programación. Usted sólo puede proporcionar el modelo para el programa que va a resolver  y le dará el resultado.

Como ya se dijo, lp_solve puede ser llamado desde muchos lenguajes de programación. Entre ellos se encuentran en C, C + +, Pascal, Delphi, Java, VB, C #, VB.NET, Excel.

Ofrece diferentes métodos de escala para hacer el modelo numérico más estable; tiene la  capacidad de aumentar las restricciones, hacer el modelo más pequeño y más rápido para resolver.

Tiene una rutina base para determinar un punto de partida y permite el reinicio después de hacer cambios en el modelo y continúa desde la última solución encontrada.

lp_solve es un solver  libre  de  programación que resuelve los problemas basándome  en el método simplex modificado y el método Branch-and-bound para los enteros. Además este solver contiene código fuente completo, ejemplos y manuales.

lp_solve resuelve problemas de programcion lineal, (mixto) enteros / binarios, semi-continuo y conjuntos ordenados especiales (SOS) modelos.

A través del algoritmo Branch-and-bound, se puede manejar variables de tipo entero, las variables semi-continuo  y los conjuntos ordenados especiales .

Sacado de _http://lpsolve.sourceforge.net/5.5/

LA IO EN OPERACIONES MILITARES

En esta ocasión nos correspondió consultar sobre aplicaciones de las teorías de colas en las fuerzas militares,  no ha sido fácil encontrar información sobre lo que se no ha pedido, ya que como todos sabemos hemos visto aplicaciones de teorías de colas en filas de bancos, supermercados, etc. pero nos realizamos un gran cuestionamiento y es ¿Cómo aplicaríamos los conceptos sobre teoría de colas que hemos ido adquiriendo como futuros ingenieros industriales, para solucionar los problemas presentes en las fuerzas militares?

La IO surgió durante la segunda guerra mundial aproximadamente entre los años 1939 y 1945. En este tiempo había una gran necesidad de administrar los recursos ya que había un gran conflicto entre países.

La fuerza aérea Británica formo el primer grupo que desarrollaría métodos cuantitativos para resolver estos problemas operacionales y bautizo a sus esfuerzos como investigación operacional:

Poco después las fuerzas armadas estadounidenses formaron un grupo similar, compuesto por científicos, físicos e ingenieros.

Un tema bastante polémico que ha traído consigo a lo largo del tiempo  controversia, son las guerras y todo lo que tiene que ver con los conflictos armados. A medida que los años han transcurrido los problemas que giran alrededor de un país van aumentando, ya sea en los polito, económico, social, religión, etc.

Para cada problema hay una solución de acuerdo a la gravedad e intensidad de este, asi mismo se le tiene que encontrar una gran solución. Para acabar con las guerras nacieron las fuerzas militares, ¿Qué función cumplen las fuerzas militares?

 Las Fuerzas Militares son las instituciones castrenses de tierra, mar y aire, de una República; están bajo el planeamiento y dirección estratégica del Comando General de las Fuerzas Militares de cada país, están conformadas por Ejército, Armada y Fuerza Aérea.

Toquemos el tema de las fuerzas militares de Colombia estas tienen como misión Defender la soberanía, la independencia, la integridad del territorio nacional y el orden constitucional, para proteger la vida, honra, bienes, creencias y demás derechos y libertades, asegurando el cumplimiento de los deberes sociales del Estado y de los particulares.

Las fuerzas militares de Colombia también tienen una visión y es ser una organización sólida, estructurada y altamente capacitada para conducir con eficacia operaciones conjuntas prolongadas en cualquier parte del territorio nacional, tendientes a mantener la soberanía, independencia, la vigencia de la Constitución, el ejercicio la ley, el funcionamiento de las instituciones y a garantizar la protección de la población y sus recursos así como para participar con fuerzas de otros países en operaciones combinadas de mantenimiento de la paz internacional.

A partir de  la segunda guerra mundial surge la investigación de operaciones por la necesidad de utilizar un sistema de diseño y utilización óptima de un nuevo sistema de detección y advertencia prematura denominado radiofrecuencia por parte de los militares para comunicarse con sus subalternos y superiores; poco después este avance sirvió para el análisis de todas las fases de las operaciones nocturnas, y el estudio se constituyó en un modelo de los estudios de investigación de operaciones que siguieron; el surgimiento de esta rama ha sido el desarrollo de múltiples teorías, pues esta ha sido fundamental en el desarrollo de diversos problemas organizacionales y empresariales; hoy día es utilizada por grandes compañías mediante la utilización de software, mecanismos para la planificación de producción, control de inventarios, etc.

Una de las teorías más importante que ha desarrollado la investigación de operaciones en el transcurso de los años ha sido la teoría de colas, pues esta tiene múltiples aplicaciones donde podemos resaltar las siguientes: solución de problemas referentes al congestionamiento del tránsito, el servicio de máquinas sujetas a imperfectos, la determinación del nivel de la mano de obra, la programación del tráfico aéreo, el diseño de empresas, la programación de la producción y la administración de hospitales. En este artículo trataremos la teoría de  colas y las aplicaciones de esta en el ámbito de las operaciones militares.

Por medio de la investigación de operaciones, utilizamos la teoría de colas con fin de crear modelos que permitan la organización y buen funcionamiento de las bases aéreas, con el fin de controlar el tráfico aéreo para realizar el debido control aéreo para la defensa de operaciones militares.

Entrevista al Ingeniero de ecopetrol William Bendeck

En esta ocasión tuvimos la placentera  oportunidad de entrevistar al ingeniero William Bendek, el cual es ex alumno de la Universidad Tecnológica de Bolívar, lugar donde nos estamos formando nosotros como ingenieros.

En esta entrevista nos cuenta como ha sido su trayectoria como profesional  y  como lo ha ayudado la investigación de operaciones en el desarrollo de su experiencia laboral; también nos cuenta  lo que tuvo que enfrentar al salir de la universidad y no contar con software especializado  y vivir la escasa  presencia de los computadores.

Por tanto los invitamos a que vean nuestra entrevista y se enteren como pudo sobrepasar todas estas limitaciones el ingeniero William Bendek.

GRID en Optimización

La tecnología actual, y principalmente la informática, ha contribuido de forma única a la resolución de millones de problemas en diferentes ámbitos y disciplinas, constituyendo hoy en día el motor de procesamiento y fuente de recursos absolutamente imprescindible.

Desde sus orígenes, la informática ha visto la luz de su evolución en las actividades científicas, más precisamente en sus necesidades de almacenamiento y procesamiento de datos. Y si bien en la mayoría de los casos la ciencia y otra variedad de disciplinas han visto satisfechos sus requerimientos, aún quedan desafíos abordables que esperan a ser atendidos. Un claro ejemplo es la capacidad de procesamiento requerida en ambiciosos proyectos de investigación científica, simulaciones a gran escala, toma de decisiones a partir de grandes volúmenes de información y cientos de casos imaginables que no encuentran una solución, o quizá parte de ella, en las herramientas disponibles en la tecnología actual.

Este artículo está basado en la  “computación grid” (En castellano: rejilla, tramado, entrelazado, enrejado). Varios conceptos similares coexisten acerca de qué es un grid. Uno de ellos, elaborado por el Grid Computing Information Centre, una de las asociaciones dedicada exclusivamente al desarrollo de esta tecnología, llama grid a un “tipo de sistema paralelo y distribuido que permite compartir, seleccionar y reunir recursos ‘autónomos’ geográficamente distribuidos en forma dinámica y en tiempo de ejecución, dependiendo de su disponibilidad, capacidad, desempeño, costo y calidad de servicio requerida por sus usuarios”. Según esta definición, se busca aprovechar la sinergia que surge de la cooperación entre recursos computacionales y proveerlos como servicios.

La aplicación de Grid en la que vamos a profundizar es en la optimización. Al optimizar procesos cuyo comportamiento no está determinado a priori, es necesario considerar la incertidumbre asociada a la predicción de dicho comportamiento. Esto conlleva la construcción de modelos de gran tamaño que tengan en cuenta esa incertidumbre y ofrezcan resultados que sean óptimos frente al abanico de situaciones posibles. Ejemplos de este tipo de problemas  son la planificación y operación de sistemas eléctricos, la planificación de la producción, la logística del transporte, la gestión de carteras de valores… Como consecuencia de su gran tamaño, en muchas ocasiones es necesario descomponer los problemas de optimización estocástica para poder resolverlos. Las posibilidades que ofrecen los grid para resolver estos problemas son muy importantes, las cuales son entornos de cálculo distribuido que reúnen gran cantidad de recursos de cálculo.

Los entornos grid son sistemas de cálculo distribuido formados por gran cantidad de equipos que se emplean como un gran ordenador virtual. Las características que definen un grid son:

• Está compuesto por una gran cantidad de equipos que pueden tener características muy diferentes en cuanto a prestaciones hardware y de la plataforma sobre la que se ejecutan.
• Estos equipos pueden estar dispersos geográficamente en las distintas organizaciones que participen en ese grid, lo que complica su gestión y coordinación.
• Los equipos están disponibles de forma dinámica, porque como medio de comunicación se emplea habitualmente Internet, que no fue diseñado para mantener unos requisitos de fiabilidad. Además, ni el número de equipos ni su estado de carga es conocido a priori por el usuario cuando lanza trabajos al grid.
• Es un sistema que debe ser escalable, es decir, debe estar pensado para poder crecer de tamaño con facilidad, ya que su objetivo es agrupar la mayor cantidad posible de recursos.

Por encima de los componentes físicos del grid (ordenadores, red de comunicaciones y otros recursos disponibles) se encuentra un middleware que es el software encargado de su gestión. La estructura de este software de gestión puede tener distintos grados de complejidad en función de las necesidades y dimensiones del grid en el que se ejecute, pero por lo general consta de al menos estos componentes.

ü  Un gestor que mantiene una lista de los recursos disponibles en el grid y que los asigna a las peticiones que reciba.

ü  Un componente que ejecuta los trabajos en cada uno de los equipos de cálculo.

ü  Otro componente que permite el acceso de las aplicaciones al grid, teniendo en cuenta la política de seguridad del sistema.

El método por el cual se utilizan los entornos grid para resolver problemas de optimización, consiste en la descomposición por escenarios completos, esto permite resolver el subproblema de cada escenario de forma independiente y asignar cada subproblema a un equipo diferente. En la resolución de cada subproblema se realizan dos tipos de cálculos:

•  En primer lugar, se resuelve el subproblema de cada escenario completo.
• En segundo lugar, se procede a calcular las consecuencias de las desiciones propuestas por los demás subproblemas, como si el propio subproblema fuese en esta ocasión el problema esclavo de los demás. Para esto se modifica el subproblema, eliminando los nodos comunes con nada uno de los demás escenarios, y se resuelve el problema resultante para las propuestas de los subproblemas de esos escenarios.

Con este algoritmo de solución se combinan varias resoluciones tradicionales simultáneas. El segundo punto conlleva un coste computacional adicional que no tiene sentido si este procedimiento no puede ser resuelto en paralelo. Sin embargo, por medio del cálculo paralelo se distribuye esa carga computacional y puede obtenerse mejoras en el tiempo total de ejecución, como se mostrara en el apartado de resultados. Para conseguir esta paralelización, se envía cada subproblema a un equipo, que se encarga de ejecutar las dos fases del cálculo que se han comentado para su subproblema: primero se calcula una nueva propuesta de decisiones propuestas por los demás escenarios en la iteración anterior. Este proceso iterativo continúa hasta que se alcanza una precisión suficiente en los valores de las soluciones de los subproblemas, que significa que se ha conseguido un acuerdo suficiente en los valores de las variables comunes a los diferentes escenarios.

REFERENCIAS BIBLIOGRÁFICAS

• www.icai.es/publicaciones/anales_get.php?id=1537. Optimización bajo incertidumbre. Técninas de descomposición y aplicación en Grid.

BITÁCORA II

El parcial se iba a realizar el día jueves 3 de Noviembre, pero se adelanto para el 27 de Octubre debido a que un grupo de estudiantes para la primera semana de este mes empezarían una ruta académica; con la colaboración del profesor la fecha fue cambiada.

Llego el tan esperado día y el segundo parcial de investigación de operaciones II tenia a todos los estudiantes con expectativas de lo que podía salir en este examen.

A la 1:00pm todos se dirigieron al 4 piso a esperar las indicaciones del profesor; como el salón en el que íbamos a realizar el examen y por supuesto las reglas del juego.

Como el profesor había comunicado que el examen se realizaría con portátil, absolutamente todos hicieron caso a esta sugerencia, ya que era lo más conveniente al realizar los ejercicios de los temas expuestos en clase.

El tiempo pasaba y el profesor nada que llegaba, los nervios inundaban aun más a cada uno de los estudiantes, hasta que a la 1:49pm el profesor llego con las hojas de parcial en la mano diciendo que el examen se realizaría en el salón donde todos los jueves dicta la clase. Por supuesto los estudiantes se dirigieron al salón de siempre,  se acomodaron, hasta que el profesor entrego la hoja de los ejercicios y la hoja verde de la sustentación de los puntos.

El parcial consto de dos puntos los cuales abordaban lo visto en todo el segundo corte, LAS CADENAS DE MARKOV, resolviendo este examen se ponían en practica las temáticas explicadas por el profesor sobre este tema.
El tiempo destinado por el profesor para hacer el parcial era de treinta minutos,  pero debido a que los estudiantes no pudimos realizarlo en tan corto tiempo, este fue prolongado. 

El profesor comento a todos los estudiantes, que tenían que analizar e interpretar más, ya que contaban con todas las herramientas para resolver los ejercicios del examen, como excel y mas sin embargo no lograbamos desarrollarlo.

El profesor nos dio más tiempo del que el se había propuesto, a lo ultimo dijo que daba 5 minutos mas y tenían todos que entregar.

Pasaron los 5 minutos y nadie había terminado el parcial, nadie quería entregar, el profesor ya un poco molesto salio del salón y dijo que si no lo entregaban el examen antes de que se fuera no lo iba a recibir.

Empezaron entregar unos, mas no todos, el profesor decidió salir del salón, haciendo que los estudiantes salieran corriendo a entregarle el examen parcial.

Cuando todos entregaron el profesor explico como se realizaban los dos ejercicios, afirmando que esto era muy sencillo, que falto más comprensión, por parte de los alumnos.

Ya para terminar nos dijo que estuviésemos pendiente del taller magistral que iba a subir en we-connect y que a partir del día que lo subiera, tendríamos una semana para entregar dicho taller.

Asi finalizo la clase del 27 de octubre de investigación de operaciones II, unos desanimados, otros no tanto, pero todos con ganas de saber los resultados obtenidos.

REDISEÑO DE TAMAÑO Y LOCALIZACIÒN DE INVENTARIO DE SEGURIDAD EN LÌNEA DE PRODUCCÍON DE IMPRESORAS PARA CUMPLIR METAS DE PRODUCCIÓN

Anteriormente la compañía pretendía utilizar un sistema de simulación para mejorar el funcionamiento del sistema pero se dio cuenta que no era lo suficientemente rápido y confiable para satisfacer sus objetivos de producción.

Dada la circunstancia HEWLETT PACKARD y El Instituto Tecnológico de Massachusetts emprendieron un proyecto en busca de soluciones, utiliza la investigación de operaciones para mejorar el diseño de la producción en sus impresoras de forma eficaz y rápida.

Ellos implementaron la tecnología que consistía en un  conjunto de algoritmos para analizar y diseñar sistemas de producción, la cual fue bastante exitosa porque permitió la articulación del equipo de diseño HP-MIT para evaluar muchos diseños rápidamente. Esto les proporcionó la flexibilidad para experimentar y probar su intuición sobre el comportamiento del sistema.  Se redujo el tiempo de mercadeo y llevó a un diseño más robusto y optimizado.

Pero HP necesitaba también lograr otros objetivos específicos, entre ellos satisfacer la demanda y la cuota en el mercado, proteger la reputación de calidad y servicio, lograr el crecimiento de los ingresos y mantener la forma de gestión que mantiene el empleo estable.

Análisis del modelo matemático utilizado.

Los sistemas de producción están en muchos casos organizados por centros de trabajo o líneas de flujo que funcionan en serie y están separados por buffers,  en la Figura se puede ver una línea de tres máquinas, los cuadrados representan las máquinas y los círculos los buffers. El material se mueve en la dirección que indican las flechas, el material entra a la máquina 1 y se realiza un proceso en el cual se modifica, pasa entonces a un buffer, donde esperará para ser procesado en la máquina 2, y así sucesivamente, hasta que sale de la línea.

El flujo de material puede ser interrumpido por fallas en alguna máquina y por variaciones en los tiempos de operación de las máquinas.  Se instalan los buffers con el fin de mejorar el desempeño del sistema, es decir, amortiguar las interrupciones y tratar de garantizar un mayor nivel promedio de producción; pero su utilización requiere de inversión monetaria y además necesita espacio, lo cual puede resultar bastante costoso, sin mencionar que se aumentan las unidades en inventario, pues cada buffer es un inventario temporal. Muchas personas se han dedicado a analizar el comportamiento de este tipo de líneas de producción, donde tienen en cuenta diferentes limitaciones, como lo puede ser por ejemplo, la poca fiabilidad o los tiempos de operación variables en cada máquina, todo esto con mi-ras a desarrollar métodos de optimización por medio de algoritmos que permiten calcular número y tamaño óptimo de buffers.

Hewlett Packard contó con la ayuda del Doctor Stanley Gershwin del Instituto de Tecnología de Massachusetts MIT, quien trabajó en conjunto con Mitchell Burman, Curtis Suyematsu, entre otros, y ha dedicado sus estudios al desarrollo de este tipo de algoritmos, enfocados a optimización de espacio y buffers. El algoritmo que se utilizó en el mejoramiento  del diseño de la línea de producción automatizada de impresoras de inyección de tinta, se basa en uno desarrollado por Dallery-David-Xie, denominado DDX, el cual fue ampliado y tomó el nombre de “Accelerated Dallery-David-Xie” o ADDX.

Introducción al algoritmo A-DDX

El algoritmo DDX fue desarrollado por Dallery, David y Xie y fue mejorado por Burman bajo el nombre de DDX Acelerado (A-DDX). El algoritmo utiliza un método de descomposición del sistema como se muestra en la Figura. Se descompone el sistema completo en subsistemas simples de 2 máquinas y un buffer. El algoritmo utiliza las características reales de operación, estos serán los parámetros de entrada Tiempo Medio Entre Falla (TMEF), Tiempo Medio Para Reparar (TMPR) y el tamaño N de cada buffer. El algoritmo entrega como resultado la tasa de producción media del sistema y la magnitud del Stock Medio Permanente (SMP) de cada buffer, que se explica más abajo.

Se tienen k_M máquinas y k_B buffers en una línea de producción que se descompone en    k_M – 1 conjuntos L(1)(i=1,2,…,K_M -1), conformados por un buffer b(i) dos máquinas (M_u (i), que alimenta el buffer b(i); y M_d (i), que se alimenta del buffer b(i), (se denota también como b(i,j) si se alimenta de la máquina M_i y alimenta a la máquina M_j).

Cada máquina M_i tiene tres parámetros:

La producción media cuando no está bloqueada o subalimentada es µ_i, lo que quiere decir que en un intervalo de tiempo σ² t, M_i transfiere µ_i σ² t del buffer b(i-1,i) al buffer b(i,i+1).

Cuando una máquina M_I está operando y no está subalimentada o bloqueada, la probabilidad de que falle en un intervalo de tiempo σ² t es p₁ σ² t.

Cuando una máquina M_i falla, la probabilidad de que sea reparada en un intervalo de tiempo σ² t es r₁ σ² t.

Cada buffer b(i,j) ob(i)tiene un solo parámetro: su capacidad, denotado por N_i.

GUROBI OPTIMIZATION

Gracias al avance computacional que se ha dado en los últimos 20 años, en programación lineal, cuadrática y mixta; se han encontrado soluciones eficaces solución para problemas de optimización.

Esto se ha dado mediante el uso de programas de alto rendimiento que proporcionan solución a dichos problemas; entre estos se encuentra GUROBI, un software basado en últimas tecnologías para resolver problemas de optimización, en programación lineal (LP), programación cuadrática (QP) y la programación entera mixta (MILP y MIQP). Que fue diseñado desde cero para aprovechar modernos procesadores multi-core.

Para la resolución de los modelos LP y QP, el Optimizador de Gurobi incluye implementaciones de alto rendimiento del método simplex, el método dual simplex, y un solucionador de barrera paralela. Para los modelos MILP y MIQP, el Optimizador de Gurobi incorpora los últimos métodos, incluyendo los planos de corte y la heurística.

Gurobi es compatible con el AIMMS , AMPL , GAMS , MPL, Microsoft Solver Foundation, Frontline Systems y Tomlab sistemas de modelización.

El optimizador de Gurobi está escrito en C y es accesible desde varios idiomas. Además de una interfaz potente e interactivo de Python, un simple ejecutable de línea de comandos y una interfaz orientada a la matriz C, que proporcionan orientación a objetos interfaces de C + +, Java, Python.

Este aprovecha al máximo la última matemáticas y las mejoras en las metodologías, así como avances en el hardware moderno de computación de escritorio y entornos de programación.

Si deseas descargar GUROBI u obtener más información, puedes acceder a: http://www.gurobi.com/

Datos curiosos:

·         Gurobi lleva el nombre de sus fundadores: Zonghao Gu, Eduardo Ro thberg y Robert Bi xby.

Bixby fue también el fundador de CPLEX (tecnología de información matemática que resuelve problemas de  programación entera y   programación lineal utilizando varios algoritmos alternativos, para tomar decisiones que buscan mejorar la eficiencia, reducir costos y aumentar la rentabilidad.), mientras que Rothberg y Gu dirigió el equipo de desarrollo de CPLEX durante casi una década 

Más información: http://www-01.ibm.com/software/integration/optimization/cplex-optimizer/

·        En Abril del presente año se lanzo la versión 4.5, Gurobi, la cual ofrece una amplia gama de opciones de licencias innovadoras. Estas incluyen las licencias de prueba gratuita, libre de licencias académicas, Pay-By-The Day-, y la nube Gurobi.

Las licencias comerciales se basan en el número de sockets de CPU utilizado, y no están vinculados al número de núcleos de procesamiento utilizados.

COMO HACER EFECTIVA LA AYUDA HUMANITARIA POR MEDIO DE LA INVESTIGACIÓN DE OPERACIONES

Para reconocer las aplicaciones de la investigación de operaciones en las ayudas humanitarias debemos recordar dos conceptos claves de esta actividad, primero ¿Qué es la investigación de operaciones?, la investigación de operaciones es una rama de las matemáticas, aplicada por lo ingenieros que consiste en el uso de modelos matemáticos, estadística y algoritmos con objeto de realizar una toma de decisiones, trata del estudio de problemas reales complejos, con la finalidad de conseguir una solución óptima es decir la solución que más nos conviene. Es necesario tener en cuenta la escasez de los recursos, para determinar cómo se pueden optimizar los procesos, ya sea maximizar beneficios o minimizar costos.


Por otro lado el segundo concepto clave necesario para explicar este es ¿Qué son ayudas humanitarias?,
Esta forma de ayuda responde a las necesidades básicas o de urgencia: hambre, hambruna, salud, reconstrucción de las infraestructuras tras un siniestro, educación, protección de la infancia y poblaciones desfavorecidas, construcción o saneamiento de las redes de agua, construcción de las redes de comunicación, etc. Normalmente se distingue la ayuda humanitaria de urgencia de la cooperación para el desarrollo en función del contexto y las necesidades de cada país.

Luego de haber explicado estos dos conceptos, podemos encontrar la relación que existe entre estos, con el fin de convertir la investigación de operaciones en una herramienta que facilite la realización de ayudas humanitarias.

El propósito de una ayuda humanitaria es que por medio de una cadena de suministros de emergencia, se pueda abastecer a la población afectada por desastres naturales y/o desastres provocados por el hombre, con el fin de minimizar el sufrimiento humano y la muerte. Al igual que en cualquier cadena de suministros comercial, en la ayuda humanitaria el flujo de suministros a través de una cadena de socorro, se presenta en una serie de envíos de larga y de corta distancia. El sistema de distribución utilizado en la ayuda humanitaria depende de las características de cada situación.


La distribución de suministros de emergencia, para una operación de socorro típica, tiene participación de actores internacionales, y consiste en que los suministros de ayuda, inicialmente llegan desde diferentes lugares del mundo a un centro primario (puertos, aeropuertos). Luego los suministros se envían a un centro secundario (grandes almacenes, centros de recolección en las ciudades), donde se almacenan, ordenan y se transfieren a centros de tercer nivel (centros de distribución local y temporal). Por último, los centros locales de distribución (LDCs), entregan los suministros de ayuda a los beneficiarios. Esta última distribución, tiene el nombre de distribución de última milla, que consiste en la última distribución realizada desde los LDCs hasta las personas en las zonas afectadas (lugares de la demanda), en donde se deben distribuir los suministros, y retroalimentar la cadena.

Los problemas logísticos en la distribución de la última milla, generalmente se derivan de las limitaciones relacionadas con los recursos de transporte y suministros de emergencia, las dificultades debido a la falta de coordinación entre los ayudantes de emergencia, y otras veces debido a la dañada infraestructura de transporte.


La ayuda humanitaria se convierte en un reto para las agencias, con el fin de que todo el proceso lleve un desarrollo eficaz y eficiente. La investigación de operaciones, es la herramienta adecuada para tomar decisiones, y plantear el modelo correcto a la hora de ayudar a los más necesitados.

Las principales decisiones operativas relacionadas con la distribución de la última milla son la asignación de suministros de ayuda, la programación de la entrega del vehículo, la ruta de los vehículos, y la asignación de la oferta efectiva en cada uno de los lugares. Por otro lado, la demanda es de vital importancia en la distribución de ayudas de emergencia, debido a las altas apuestas asociadas a la demanda insatisfecha y/o satisfecha, pero tarde. La tarea se hace difícil, por consecuencia de las estrictas limitaciones financieras.

El problema de distribución de última milla es una variante del problema de enrutamiento de inventario (IRP). Las principales decisiones en el IRP son los tiempos de entrega al cliente, el número de elementos que se entrega en cada visita, y las rutas de entrega. La asignación equitativa entre la oferta y los puntos de demanda es una preocupación importante. Se considera que en un sistema de distribución de última milla, en la que un país menos adelantado almacena y distribuye suministros de emergencia, a una serie de lugares de la demanda, con un conjunto fijo de los vehículos, se proponen dos fases de modelado para determinar un calendario de entrega de cada vehículo, y tomar decisiones de asignación de inventario, teniendo en cuenta la oferta, la capacidad del vehículo, y las restricciones de tiempo de entrega. El objetivo es reducir al mínimo la suma de los costos de transporte y gastos de penalización por demanda insatisfecha.


En la ayuda humanitaria se ha utilizado la investigación de operaciones con el fin de crear un modelo de programación lineal, para determinar el número de visitas a cada zona damnificada, para satisfacer la demanda y reducir al mínimo el costo de transporte, o maximizar la cantidad de alimentos entregados. El modelo, no puede manejar las contingencias de la oferta insuficiente, y se llega a la conclusión de que el problema es demasiado complejo, para los modelos clásicos de investigación de operaciones y técnicas de solución. Se debe combinar la heurística de la investigación de operaciones con técnicas de inteligencia artificial, para desarrollar una herramienta de soporte de decisiones para la asignación y distribución de suministros.

Se han presentado casos, en donde las sociedades damnificadas por no contar con el conocimiento, ni con los recursos, a la hora de ocurrir un desastre natural, no saben como reaccionar, y no recurren a la investigación de operaciones como un medio para salir de la crisis, sino que por el contrario, la cura termina peor que la enfermedad, y a la hora de abastecer a las personas necesitadas, el desorden es tal, que se pierden muchas veces los suministros por mala distribución y por mala organización. A continuación encontramos imágenes de desastres, en donde el panorama ha sido desalentador, y por ser tan grande el desastre, la distribución y organización ha sido demorada y desorganizada.

REFERENCIAS:

· http://faculty.washington.edu/benita/paper22.pdf

ALGORITMOS DE NUBES DE PARTÍCULAS PARA RESOLVER PROBLEMAS ENTEROS

Muchos problemas de optimización tienen una alta complejidad, debido a que generalmente son problemas de NP-duras y también porque el tiempo que se posee para resolverlos es muy limitado;  por tanto la informática se ha convertido en pieza clave para la resolución de estos, usando métodos exactos y heurísticos, los cuales son capaces de encontrar muy buenas soluciones en un tiempo y consumo de recursos razonables.

 

Entre las técnicas heurísticas, se encuentran los algoritmos basados en cúmulos de partículas, concretamente el método denominado Particle Swarm Optimization (PSO).

 

Esta técnica fue desarrollada por el psicólogo-sociólogo Jammes Kennedy y por el ingeniero electrónico Russell Eberhart en 1995, fundamentándose en experimentos con algoritmos que modelaban el  comportamiento en vuelo observado en algunas especies de pájaros, o el comportamiento de los bancos de peces, incluso las tendencias sociales en el comportamiento humano.

En este algoritmo, cada individuo, llamado partícula, se va moviendo en un espacio multidimensional que representa su espacio social. Cada partícula tiene memoria mediante la que conserva parte de su estado anterior. Cada movimiento de una partícula es la composición de una velocidad inicial aleatoria y dos valores ponderados aleatoriamente: individual (la tendencia de las partículas de preservar su mejor estado anterior) y social (la tendencia a moverse hacia vecinos con mejor posición).

Debido a su planteamiento, este tipo de algoritmo se adapta muy bien a problemas de programación lineal y entera.

Este problema se plantea de la siguiente manera: se supone que una bandada de aves busca comida en un área y que solamente hay una pieza de comida en dicha área. Los pájaros no saben dónde está la comida pero sí conocen su distancia a la misma, por lo que la estrategia más eficaz para hallar la comida es seguir al ave que se encuentre más cerca de ella. PSO utiliza este escenario para resolver problemas de optimización.

Cada solución (partícula) es un ave en el espacio de búsqueda que está siempre en continuo movimiento y que nunca muere.

El modelo del PSO, es:

: velocidad de la partícula i en la iteración k.

ⱳ: factor inercia.

: son ratios de aprendizaje (pesos) que controlan los componentes cognitivo y social.

rand1; rand2 : números aleatorios entre 0 y 1.

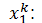: posición actual de la partícula i en la iteración k.

pBesti : mejor posición (solución) encontrada por la partícula i hasta el momento.

gi : representa la posición de la partícula con el mejor pBest_fitness del entorno de pi (lBest o localbest) o de todo el cúmulo (gBest o globalbest).

El modelo se representa en las siguientes ecuaciones:

La primera ecuación, refleja la actualización del vector velocidad de cada partícula i en cada iteración k.

Tipos de Algoritmos de PSO.

Existe muchos tipos de PSO que atienden diversos factores, como lo son: según la importancia de los pesos cognitivo, social y según el tipo de vecindario utilizado.

Ya dependiendo de la influencia de los factores cognitivo y social sobre la dirección de la velocidad que toma una partícula en el movimiento identifica cuatro tipos de algoritmos:

•   Modelo Completo: Tanto el componente cognitivo como el social intervienen en el movimiento.
•         Modelo sólo Cognitivo: Únicamente el componente cognitivo interviene en el movimiento.
•         Modelo sólo Social: Únicamente el componente social interviene en el movimiento.
•        Modelo sólo Social exclusivo: La posición de la partícula en sí no puede ser la mejor de su entorno.

·        

Por otra parte desde el punto de vista del vecindario es decir, la cantidad y posición de las partículas que intervienen en el cálculo de la distancia en la componente social, se clasifican dos tipos de algoritmos: PSO Local y PSO Global.

En el PSO Local, se calcula la distancia entre la posición actual de partícula y la posición de la mejor partícula encontrada en el entorno local de la primera. El entorno local consiste en las partículas inmediatamente cercanas en la topología del cúmulo.

Para el PSO Global, la distancia en el componente social viene dada por la diferencia entre la posición de la partícula actual y la posición de la mejor partícula encontrada en el cúmulo completo. La versión Global converge más rápido pues la visibilidad de cada partícula es mejor y se acercan más a la mejor del cúmulo favoreciendo la intensificación, por esta razón, también cae más fácilmente en óptimos locales.

Topologías del Cúmulo de Partículas.

Hay que resaltar algo muy importante, y es la manera en que una partícula interacciona con las demás partículas de su vecindario. El desarrollo de una partícula depende tanto de la topología del cúmulo como de la versión del algoritmo. Las topologías definen el entorno de interacción de una partícula individual con su vecindario. La propia partícula siempre pertenece a su entorno. Los entornos pueden ser de dos tipos:

• Geográficos: se calcula la distancia de la partícula actual al resto y se toman las más cercanas para componer su entorno.
• Sociales: se define a priori una lista de vecinas para partícula, independientemente de su posición en el espacio.

Un problema habitual de los algoritmos de PSO es que la magnitud de la velocidad suele llegar a ser muy grande durante la ejecución, con lo que las partículas se mueven demasiado rápido por el espacio. El rendimiento puede disminuir si no se fija adecuadamente el valor de vmax, la velocidad máxima de cada componente del vector velocidad.

Por último podemos decir que este algoritmo se aplica en diferentes campos de investigación. Entre ellos están: la optimización de funciones numéricas, el entrenamiento de redes neuronales, el aprendizaje de sistemas difusos, el registrado de imágenes, el problema del viajante de comercio e ingeniería química. 

REFERENCIAS:

• Algoritmos Basados en Cúmulos de Partículas Para la Resolución de Problemas Complejos
• Autor: José Manuel García Nieto
• Directores: Enrique Alba Torres y Gabriel Jesús Luque Polo
• septiembre de 2006